Manual de matemáticas
Identidades notables
Identidades trigonométricas
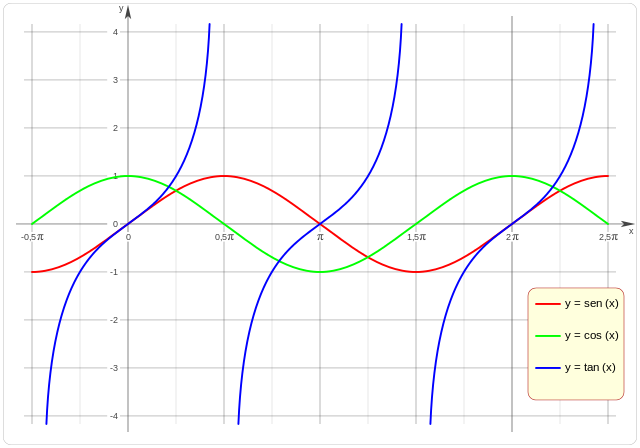
Identidad pitagórica: $$ \sin^2(a) + \cos^2(b) = 1 $$ Seno y coseno de la suma: $$ \begin{align} \sin(a \pm b) &= \sin(a)\cos(b) \pm \cos(a)\sin(b) \\[1ex] \cos(a \pm b) &= \cos(a)\cos(b) \mp \sin(a)\sin(b) \\[1ex] \tan(a \pm b) &= \frac{ \tan(a) \pm \tan(b) }{ 1 \mp \tan(a)\tan(b) } \\[1ex] \end{align} $$ De suma a producto:
Propiedades del producto vectorial
$$ \begin{align} \boldsymbol{A} \times \boldsymbol{B} &= - \boldsymbol{B} \times \boldsymbol{A} \\ (\alpha \boldsymbol{A}) \times \boldsymbol{B} &= \boldsymbol{A} \times (\alpha \boldsymbol{B}) \\ \boldsymbol{A} \times (\boldsymbol{B} + \boldsymbol{C}) &= \boldsymbol{A} \times \boldsymbol{B} + \boldsymbol{A} \times \boldsymbol{C} \\ \boldsymbol{A} \times (\boldsymbol{B} \times \boldsymbol{C}) &= (\boldsymbol{A} \times \boldsymbol{B}) \times \boldsymbol{C} \\ \boldsymbol{A} \times \boldsymbol{B} \times \boldsymbol{C} &= \boldsymbol{B}(\boldsymbol{A} \cdot \boldsymbol{C}) - \boldsymbol{C}(\boldsymbol{A} \cdot \boldsymbol{B}) \\ \end{align} $$
Álgebra
\[ A^{-1}= \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \frac{1}{det A}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \]Geometría
Las curvas cónicas: elipse/circunferencia, parábola e hipérbola. Cada curva se caracteriza por su excentricidad $e$. La ecuación de la elipse, $a$ es el semieje mayor, $b$ es el semieje menor, $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \qquad e = \sqrt{1 - \frac{b^2}{a^2}} $$ Ecuación de una elipse inclinada cuyo eje mayor forma un ángulo $\alpha$ con el eje X encajada en un rectángulo $A_x \times A_y$ y cuya trayectoria es $\left(A_x\cos(\omega t), A_y\cos(\omega t + \epsilon)\right)$ $$ \left(\frac{x}{A_x}\right)^2 + \left(\frac{y}{A_y}\right)^2 - 2\left(\frac{x}{A_x}\right)\left(\frac{y}{A_y}\right)\cos\epsilon = \sin^2\epsilon \qquad \tan(2\alpha) = \frac{2A_xA_y\cos\epsilon}{A_x^2-A_y^2} $$ de lo anterior se deduce que para conseguir una trayectoria circular $\epsilon = \pm\pi/2, \pm 3\pi/2, \pm 5\pi/2$, etc, y $A_x=A_y$
Ecuaciones
Ecuación de segundo grado
Una ecuación de segundo grado $ax^2 + bx + c = 0$ puede tener dos soluciones reales, una solución real doble o dos soluciones complejas en función del discriminante $\Delta = b^2 - 4ac$ $$ x = {-b \pm \sqrt{b^2-4ac} \over 2a} = {-b \pm \sqrt{\Delta} \over 2a} $$
- si $\Delta > 0$ hay dos soluciones reales distintas
- si $\Delta = 0$ hay una solución real doble
- si $\Delta < 0$ hay dos soluciones complejas conjugadas
Ecuación bicuadrada
Una ecuación bicuadrada $ax^4 + bx^2 + c = 0$ es una ecuación de cuarto grado y, por lo tanto, tiene 4 soluciones. Se resuelven aplicando un cambio de variable $t = x^2$ y luego resolviendo la ecuación de segundo grado resultante, cuyas soluciones son $t_1$ y $t_2$. $$ at^2 + bt + c = 0 $$ $$ \begin{aligned} x_1 &= +\sqrt{t1} \\ x_2 &= -\sqrt{t1} \\ x_3 &= +\sqrt{t2} \\ x_4 &= -\sqrt{t2} \\ \end{aligned} $$
Distribuciones de probabilidad
Distribución binómica
Si realizamos N experimentos de Bernoulli todos ellos estadísticamente independientes entre sí y con probabilidad de éxito $p$ y probabilidad de fracaso $q = 1 -p$ entonces la probabilidad de tener $n$ éxitos es \[ Binomial(n, N, p) = \frac{N!}{n! (N - n)!} p^n q^{N - n} \] La media es $E(X) = Np$ La varianza es $Var(X) = Npq$ La desviación típica es $\sigma(X) = \sqrt{Npq}$Esperanza, varianza y desviación típica
La esperanza (también llamada valor medio media) de una V.A $X$ se define como \[ E(X) = \sum_{i = 0}^{N} p_i x_i \] La varianza de una V.A. $X$ es la dispersión entorno a la media E(X) y siempre es $Var(X) \geq 0$ \[ Var(X) = \sum_{i = 0}^{N} p_i (x_i - E(X))^2 \] La desviación típica es simplemente la raíz cuadrada de la varianza, mide igualmente la dispersión entorno a la media pero sus unidades son las mismas que las de la V.A. $X$. \[ \sigma(X) = \sqrt{ Var(X) } \]Algunos desarrollos en serie
| Función | Serie |
| \[ \sum_{n = 0}^{\infty} z^n \] | \[ \frac{1}{1 - z} \] |
| \[ \sum_{n = 0}^{N} z^n \] | \[ \frac{1 - z^{N+1}}{1 - z} \] |
| \[ e^z \] | \[ \sum_{n = 0}^{\infty} \frac{z^n}{n!} \] |
| \[ \cos(z) \] | \[ 1 - \frac{z^2}{2!} + \frac{z^4}{4!} - \frac{z^6}{6!} + \ldots = \sum_{n = 0}^{\infty} (-1)^n \frac{z^{2n}}{(2n)!} \] |
| \[ \sin(z) \] | \[ \frac{z}{1!} - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \ldots = \sum_{n = 0}^{\infty} (-1)^n \frac{z^{2n + 1}}{(2n + 1)!} \] |
| \[ \cosh(z) \] | \[ \sum_{n = 0}^{\infty} \frac{ (z + 2\pi i)^{2n} }{ (2n)! } \] |
| \[ \sinh(z) \] | \[ \sum_{n = 0}^{\infty} \frac{ z^{2n + 1} }{ (2n + 1)! } \] |
| Taylor: \[ f(a + \delta x) \] | \[ f(a) + \frac{f'(a)}{1!}(\delta x)^1 + \frac{f''(a)}{2!}(\delta x)^2 + \frac{f'''(a)}{3!}(\delta x)^3 + ... \] \[ \delta x = x - a \] |
| \[ \frac{a}{1 - x} \] | \[ a + ax + ax^2 + ax^3 + ..., \text{con}\ \ 0 < x < 1 \] |
| \[ \frac{\sin\left((p+1/2)A\right)}{2\sin(A/2)} \] | \[ 1/2 + \cos(A) + \cos(2A) + \cos(3A) + \ldots + \cos(pA) \] |
Ecuaciones diferenciales ordinarias
| Descripción | Ecuación | Solución |
|---|---|---|
| $ \dot{q} = \alpha q $ | $ q(t) = q_0 e^{\alpha t} $ | |
| Aceleración constante $a$ con fuerza de rozamiento $F_r$ proporcional a la velocidad $F_r = -bv$ | $ \ddot{q} = a - b \dot{q} $ | $ \dot{q}(t) = \frac{a}{b} + (\dot{q}_0 - \frac{a}{b}) e^{-bt} $ |
| Oscilador armónico simple. Por ejemplo: péndulo simple con oscilaciones pequeñas, oscilador masa-muelle, etc. | $ \ddot{q} + \omega^2 q = 0 $ | $$ q(t) = A\cos(\omega t + \phi) $$ siendo $$ \begin{align} A &= \sqrt{q_0^2 + \dot{q}_0^2 / \omega^2 } \\ \phi &= \arccos\left( +\frac{q_0 }{A } \right) \\ \phi &= \arcsin\left( -\frac{\dot{q_0}}{\omega A} \right) \\ \phi &= \arctan\left(-\frac{\dot{q}_0 }{q_0\omega}\right) \\ \end{align} $$ |
Una Ecuación Diferencial Ordinaria Lineal con Coeficientes Constantes y Homogénea (EDOLCCH) es una ecuación del tipo $$ a_N \frac{d^N}{dt^N}x + a_{N-1} \frac{d^{N-1}}{dt^{N-1}}x + \ldots + a_1 \frac{d}{dt}x + a_0 x = 0 $$ a la que podemos asociar el siguiente polinomio $P(s)$ equivalente $$ P(s) = a_N s^N + a_{N-1} s^{N-1} + \ldots + a_1 s + a_0 $$
Teorema 1: Sean $\sigma_1, \sigma_2, \ldots, \sigma_N $ las raíces del polinomio $P(s)$, entonces una función del tipo $x = e^{\sigma_i t}$ es solución de la EDOLCCH.
Teorema 2: Si $x_1$ y $x_2$ son dos soluciones de la EDOLCCH entonces una combinación lineal $A_1x_1 + A_2x_2$ de ambas también es solución de la EDOLCCH. Las constantes ajustables se determinan mediante las condiciones iniciales o de contorno del problema.
Una consecuencia inmediata de los dos teoremas anteriores es que la solución general de la EDOLCCH es del tipo $$ x_h(t) = \sum_{i=1}^N A_i e^{\sigma_i}t $$
Sistemas de coordenadas
Cilíndricas/polares
Los vectores unitarios $\hat{r}$ y $\hat{\phi}$ no son constantes, dependen de la posicion $r$ y $\phi$ y por lo tanto hay que integrarlos y derivarlos.
Operador gradiente:
\[ \nabla = \frac{\partial}{\partial r} \hat{r} + \frac{1}{r}\frac{\partial}{\partial \phi} \hat{\phi} + \frac{\partial}{\partial z} \hat{z}\]Posición, velocidad y aceleración en cilíndricas/polares
$$ \begin{align} \mathbf{r} &= r \mathbf{u_r} + z \mathbf{u_z}\\ \mathbf{\dot{r}} &= \dot{r}\mathbf{u_r} + r\dot{\phi} \mathbf{u_\phi} + \dot{z}\mathbf{u_z} \\ \mathbf{\ddot{r}} &= (\ddot{r}-r\dot{\phi}^2)\mathbf{u_r} + (2\dot{r}\dot{\phi}+r\ddot{\phi}) \mathbf{u_\phi} + \ddot{z}\mathbf{u_z} \\ \end{align} $$Esféricas
|
|
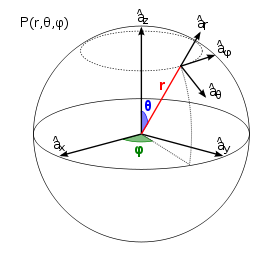
Los vectores unitarios $\hat{r}$, $\hat{\theta}$ y $\hat{\phi}$ no son constantes, dependen de la posicion ($r$, $\theta$, $\phi$) y por lo tanto hay que integrarlos y derivarlos. Forma una base dextrógira cuando se ordenan en la forma ($r$, $\phi$, $\theta$)
Paso de coordenadas esféricas a rectangulares:
$$ \begin{align} x &= r \sin\theta \cos\phi \\ y &= r \sin\theta \sin\phi \\ z &= r \cos\theta \end{align} $$De la base rectangular a la base esférica
$$ \begin{align} \mathbf{u_r} &= \cos\theta\cos\phi \mathbf{u_x} + \cos\theta\sin\phi\mathbf{u_y} + \sin\theta\mathbf{u_z} \\ \mathbf{u_\theta} &= -\sin\theta\cos\phi \mathbf{u_x} - \sin\theta\sin\phi\mathbf{u_y} + \cos\theta\mathbf{u_z} \\ \mathbf{u_\phi} &= \mathbf{u_\theta} \times \mathbf{u_r} = -\sin\phi\mathbf{u_x} + \cos\phi\mathbf{u_y} \\ \end{align} $$Operador gradiente:
$$ \nabla = \frac{\partial}{\partial r} \hat{r} + \frac{1}{r}\frac{\partial}{\partial \theta} \hat{\theta} + \frac{1}{r\sin(\theta)}\frac{\partial}{\partial \phi} \hat{\phi} $$El convenio internacional y el de EE.UU. tienen los angulos $\phi$ (azimut) y $\theta$ (colatitud) intercambiados asi que cuidado al consultarlas en la bibliografia porque varian segun el libro de texto. Las expresiones anteriores y el diagrama corresponden al convenio internacional ISO 80000-2:2009
Posición, velocidad y aceleración en esféricas
$$ \begin{align} \mathbf{r} &= r \mathbf{u_r} \\ \mathbf{\dot{r}} &= \dot{r} \mathbf{u_r} + r \dot{\theta} \mathbf{u_\theta} + r\dot{\phi}\cos\theta \mathbf{u_\phi} \\ \mathbf{\ddot{r}} &= (\ddot{r}-r\dot{\phi}^2\cos^2\theta - r\dot{\theta}^2) \mathbf{u_r} + (2\dot{r}\dot{\theta} + r\dot{\phi}^2\sin\theta\cos\theta + r\ddot{\theta}) \mathbf{u_\theta} + (2\dot{r}\dot{\phi}\cos\theta - 2r\dot{\theta}\dot{\phi}\sin\theta + r\ddot{\phi}\cos\theta) \mathbf{u_\phi} \\ \end{align} $$Rectangulares
Operador gradiente:
\[ \nabla = \frac{\partial}{\partial x} \hat{x} + \frac{\partial}{\partial y} \hat{y} + \frac{\partial}{\partial z} \hat{z} \]Aproximaciones
- Aproximación de Stirling: $ ln(x!) = x ln(x) - x $, con $ x >> 1$
- $ln(1 + y) = y$, con $ y << 1$
- $\sqrt{1 + x} = 1 + \frac{1}{2}x$, con $x$ muy pequeño (hasta orden 1)
- $\sqrt{1 + x} = 1 + \frac{1}{2}x + \frac{1}{4}x² $, con $x$ muy pequeño (hasta orden 2)
- $\sin(x) = x$, con $x$ muy pequeño
- $\cos(x) = 1-\frac{x^2}{2}$, con $x$ muy pequeño