Updated:
Modelo M/M/1/k
fork() sino que pone en una cola de espera de tamaño finito las conexiones TCP entrantes y las atiende una a una por orden de llegada (FIFO).
Por ejemplo, en la API de sockets Berkely, la llamada a int listen(int ds, int nb) permite especificar
el tamaño máximo de la cola (parámetro nb) de espera para las conexiones TCP entrantes (llamadas "tareas" a
partir de ahora). Con un sólo proceso servidor, ¿cuál es la probabilidad \(B\) de que una conexión TCP entrante
sea rechazada porque la cola esté llena?

- \(\lambda\)
- Tráfico ofrecido (tareas/s)
- \(\lambda_c\)
- Tráfico cursado (tareas/s)
- \(\mu\)
- Velocidad de servicio (tareas/s)
- \(B\)
- Probabilidad de bloqueo
- \(k\)
- Capacidad del sistema (tareas)
Si el tráfico proviene de un número muy elevado de usuarios independientes entonces se puede caracterizar estadísticamente como de [http://es.wikipedia.org/wiki/Proceso_de_Poisson Poisson]. La duración de las conexiones, por otra parte, se ha demostrado empíricamente que se puede caracterizase por ser de Pareto(m, \(\alpha\)) con \(\alpha < 2\). Así pues, podemos usar un modelo M/M/1/k(El modelo M/M/1/k es uno de los más comunes puesto que la cola de espera en un router o en un servidor siempre es finita (porque la memoria lo es). Se trata, por tanto, de un modelo de cola mixto en el que hay tanto espera como rechazo.) para tener una respuesta aproximada a la pregunta anterior.
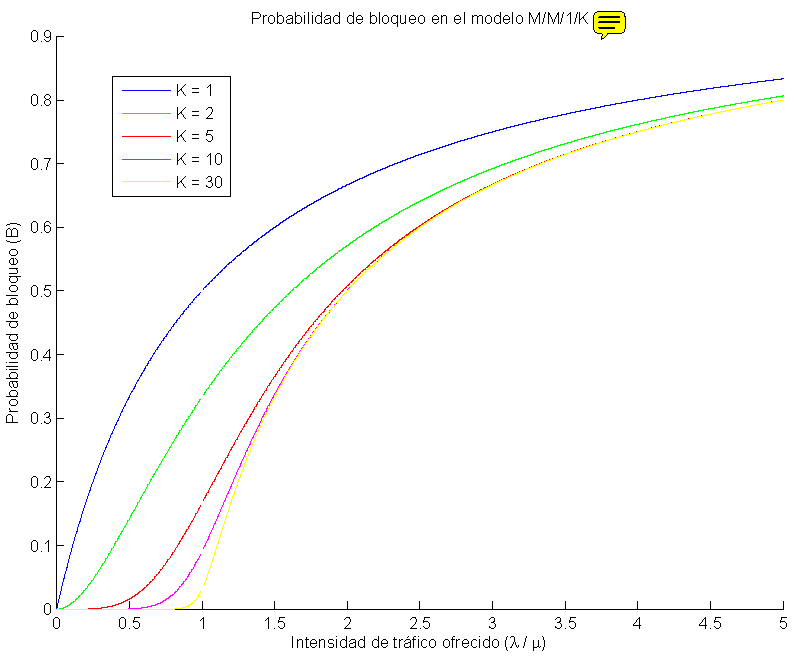
La probabilidad de bloqueo (B) de tareas que he obtenido es:
$$ B = \left\{\begin{matrix} \frac{1}{k+1} & \mbox{si } r = 1 \\ \frac{r^k(1-r)}{1-r^{k+1}}& \mbox{si } r \ne 1 \end{matrix}\right.\, $$ siendo \(r=\lambda / \mu\) la intensidad de tráfico ofrecido al sistema. Puedo por fin confirmar que el resultado al que he llegado es correcto. Después de buscar durante algún tiempo finalmente encontré un libro (ver [[#Referencias|Referencias]]) en el que aparece este modelo y, aunque no aparece la demostración, el resultado final es el mismo. Ok.Demostración
La distribución de probabilidad de ocupación del sistema se obtiene considerando al proceso de ocupación del sistema \(N(t)\) como un proceso de nacimiento y muerte(Un proceso de nacimiento y muerte es un proceso de Markov sin memoria en el que todas las transiciones son siempre a estados adyacentes) de una dimensión. Las tasas de nacimiento y muerte en cada estado son $$ \lambda_i = \lambda \ \ \ 0 \le i < k\ $$ $$ \mu_i = \mu \ \ \ 0 < i \le k\, $$
$$ p_n = p_0 \prod^n_{i=1}\frac{\lambda_{i-1}}{\mu_i} = p_0 \left(\frac{\lambda}{\mu}\right)^n = p_0 r^n\, con r = \frac{\lambda}{\mu}\, $$Utilizando que la suma de una distribución de probabilidad vale 1, despejamos \(p_0\) y usamos la suma de una progresión geométrica finita
$$ \sum^k_{n=0}p_n = 1 \rightarrow p_0 \sum^k_{n=0} r^n= p_0 \frac{1 - r^{k+1}}{1 - r} = 1 \rightarrow p_0 = \frac{1 - r}{1 - r^{k+1}}\, $$La distribución de probabilidad de ocupación del sistema es
$$ p_n = \frac{r^n(1 - r)}{1 - r^{k+1}}\, $$Por la propiedad PASTA (Poisson Arrivals See Time Averages) del proceso de llegada de Poisson, la probabilidad de bloqueo de una tarea (\(B\)) es igual a la probabilidad de bloqueo temporal (\(B_T\)):
$$ B = B_T = p_k = \frac{r^k(1 - r)}{1 - r^{k+1}}\, con r \ne 1\, $$La expresión es indeterminada en \(r = 1\), es decir, que para este valor el sistema no se encuentra en equilibrio estadístico. Esto es muy interesante y no se muy bien cómo interpretarlo. En el límite, cuando \(r \rightarrow 1\), usando la regla de L'Hôpital para deshacer la indeterminación, tenemos
$$ \lim_{r \to 1} B = \lim_{r \to 1} \frac{r^k(1-r)}{1-r^{k+1}} = \lim_{r \to 1} \frac{kr^{k-1}(1-r) + r^k(-1)}{(-1)(k+1)r} = \frac{1}{k+1} $$Suponiendo que B es una función continua, tenemos finalmente:
$$ B = \left\{\begin{matrix} \frac{1}{k+1} & \mbox{si } r = 1 \\ \frac{r^k(1-r)}{1-r^{k+1}}& \mbox{si } r \ne 1 \end{matrix}\right.\, $$La expresión muestra que B tiende a 0 cuando disminuye el tráfico o cuando aumenta el tamaño de la cola.
Gráfica
Fichero: mm1k.m
Referencias
- "Teoría de colas y simulación de eventos discretos", José Juan Pazos Arias, Andrés Suárez González y Rebeca P. Díaz Redondo, Pearson, ISBN 84-205-3675-X
- TELETRAFFIC ENGINEERING HANDBOOK