VYO - Dinámica del MAS. Amortiguación. Resonancia.
Definiciones
- Tensión mecánica
- Fuerza / Área, $\sigma = F / A$
- Módulo de Young
- Caracteriza el comportamiento de un material elástico, se define
como $Y = \frac{\sigma}{\epsilon} = \frac{F/S}{\Delta
L/L}$
siendo $\sigma$ la tensión mecánica aplicada y $\epsilon$ la deformación unitaria o relativa del material - Oscilador libre no amortiguado
- $\ddot{x} + \omega_0^2 x = 0$
- Oscilador libre amortiguado
- $\ddot{x} + 2\gamma\dot{x} + \omega_0^2 x = 0$
- Oscilador forzado no amortiguado
- $\ddot{x} + \omega_0^2 x = \frac{F_0}{m}\cos(\omega t + \alpha_0)$
- Oscilador forzado amortiguado
- $\ddot{x} + 2\gamma\dot{x} + \omega_0^2 x = \frac{F_0}{m}\cos(\omega t + \alpha_0)$
No es físicamente posible un oscilador no amortiguado. Todos tienen en mayor o menor grado un coeficiente de amortiguamiento. Los modelos no amortiguados tienen un interés principalmente matemático.
Método general para EDOs lineales homogéneas de grado 2 con coeficientes constantes
$$ \lambda^2 + 2\gamma\lambda + \omega_0^2 = 0 \\ \lambda = -\gamma \pm i\omega_\gamma \longrightarrow \lambda_1, \lambda_2 $$ $$ x(t) = C_1e^{\lambda_1 t} + C_2e^{\lambda_2 t} $$ aplicando las condiciones iniciales obtenemos un sistema de ecuaciones algebráicas con el que obtenemos $C_1$ y $C_2$
Oscilador libre no amortiguado
Es una caso particular del oscilador amortiguado (con $\gamma = 0$)
Oscilador libre amortiguado
Muelle vs amortiguador
Un muelle ejerce una fuerza directamente proporcional ($k$) al desplazamiento relativo de los extremos mientras que un amortiguador ejerce una fuerza directamente proporcional ($b$) a la velocidad relativa de sus extremos. El vector fuerza es siempre opuesto al vector velocidad. $$ \begin{align} F_k &= -k (x_2 - x_1) \\ F_b &= -b \frac{d}{dt}(x_2 - x_1) = -b (v_2 - v_1) \\ \end{align} $$
Factor de calidad $Q$ y amortiguamiento $\zeta$
Está relacionado con la energía que se pierde en cada periodo del oscilador: $$ Q = 2\pi\frac{E_{total}}{E_{perdida-por-periodo}} = \frac{1}{2}\frac{\omega_0}{\gamma} = \frac{1}{2}\frac{1}{\zeta} $$ En un oscilador armónico la energía total es $E_0 = \frac{1}{2}kA^2$ y el decaimiento de esta energía total por disipación (solo en el caso de amortiguamiento subcrítico, si no no habría oscilación) es $E(t) = E_0e^{-2\gamma t}$
Niveles de amortiguamiento $\gamma$
- Subcrítico: $\gamma^2 < \omega_0^2$
En este caso la oscilación se desvanece paulatinamente, los cruces por cero no están exactamente en el punto medio entre el mínimo y el máximo. La solución tiene la forma $$ x(t) = C e^{-\gamma t} \sin(\omega_\gamma t + \delta) = C e^{-\gamma t} \cos\left(\omega_\gamma t + \delta - \frac{\pi}{2}\right) \\ \omega_\gamma = \sqrt{ \omega_0^2 - \gamma^2 } \\ C^2 = x_0^2 + \frac{(v_0 + \gamma x_0)^2}{\omega_\gamma^2} \\ \delta = arctan\left(\frac{\omega_\gamma x_0 }{ v_0 + \gamma x_0}\right) \\ $$- tiempo de relajación $\tau$
- decremento logarítmico de la amplitud $\Delta$
- coeficiente de amortiguación $\zeta = \gamma/\omega_0$
- Crítico: $\gamma^2 = \omega_0^2$
En este caso no hay oscilación. La solución tiene la forma $$ x(t) = (A_1 + A_2 t)e^{-\gamma t} $$ - Supercrítico: $\gamma^2 > \omega_0^2$
En este caso no hay oscilación. La solución tiene la forma $$ \begin{align} x(t) &= A_1 e^{-(\gamma + \beta)t} + A_2 e^{-(\gamma - \beta)t} \\ \beta &= \sqrt{\gamma^2 - \omega_0^2} \\ \end{align} $$
Oscilador forzado no amortiguado
Es una caso particular del oscilador forzado amortiguado (con $\gamma = 0$)
Forzamiento: régimen transitorio y régimen permanente
En el modelo del oscilador forzado amortiguado la solución es realmente la suma de dos términos
- la solución de la ecuación homogénea $x_h(t)$
- una solución particular $x_p(t)$
Oscilador forzado amortiguado
Al aplicar una fuerza oscilante $F_0\cos(\omega t + \alpha_0)$ en el término independiente de la ecuación del sistema la solución tiene dos partes: $$ x(t) = \color{blue}{x_h(t)} + \color{green}{x_p(t)} = \color{blue}{C e^{-\gamma t}\sin(\omega_\gamma t + \delta)} + \color{green}{ A \sin(\omega t + \alpha_0 + \beta) } $$
- un término $x_h$ evanescente multiplicado por $e^{-\gamma t}$ que corresponde a la ecuación homogénea y por lo tanto es la misma que la del oscilador libre (amortiguado o no). Es importante durante el régimen transitorio. La amplitud $C$ y constante de fase $\delta$ depende de las condiciones iniciales ($t=0$), ojo, a dichas condiciones iniciales contribuye también la componente estacionaria $x_p(t)$
- un término $x_p$ permanente que tiene la misma frecuencia $\omega$ que la frecuencia forzante. Es el término que corresponde al régimen sinusoidal permanente. Esta componente de la solución no depende de las condiciones iniciales ($t=0$)
Vamos a ocuparnos del término permanente:
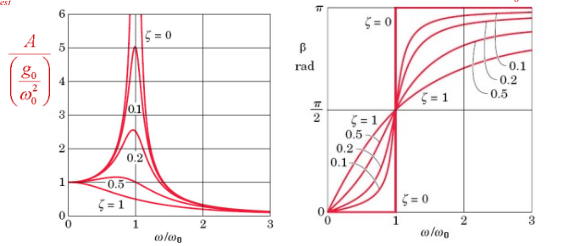
La amplitud de oscilación $A$ depende de la relación entre la frecuencia
natural $\omega_0$ y la frecuencia forzante $\omega$
$$ A = \frac{F_0/m}{\sqrt{ (\omega^2-\omega_0^2)^2 + 4\gamma^2\omega^2
}} \qquad \beta = -arctan\left( \omega^2-\omega_0^2 \over 2\gamma\omega \right) $$
Si la solución es en forma de coseno entonces hay que invertir la
fracción de la expresión de $\beta$. En la literatura se pueden
encontrar numerosas variantes de esta expresión dependiendo de si
$\beta$ aparece sumando o restando, de si es seno o coseno, etc.
Concepto de ganancia o factor de amplificación de un oscilador forzado: $$ F_{amp} = \frac{A}{\delta_{est}} = \frac{A}{\frac{F_0/m}{\omega_0^2}} = \frac{1}{\sqrt{ \left(1-(\frac{\omega}{\omega_0})^2\right)^2 + \left(2\zeta\frac{\omega}{\omega_0}\right)^2 }} $$
Energía y potencia en el oscilador forzado. Resonancia.
Potencia suministrada por la fuerza externa $$ P(t) = F(t) \dot{x}(t) $$ La potencia absorbida tiene ciclos en que es positiva y luego negativa, eso significa que la energía absorbida por el sistema luego se devuelve a la fuente. La potencia disipada es justamente la diferencia, por tanto, potencia absorbidad y potencia disipada no son lo mismo.
Tabla resumen de soluciones
| Tipo | Ecuación | Solución |
|---|---|---|
| Oscilador libre no amortiguado | $ \ddot{q} + \omega^2 q = 0 $ | $$ q(t) = A\cos\left(\omega t + \phi\right) = A\sin\left(\omega t + \phi + \frac{\pi}{2}\right) $$ siendo $$ \begin{align} A &= \sqrt{q_0^2 + \dot{q}_0^2 / \omega^2 } \\ \phi &= \arccos\left( +\frac{q_0}{A} \right) = \arcsin\left( -\frac{\dot{q_0}}{\omega A} \right) = \arctan\left(-\frac{\dot{q}_0 }{q_0\omega}\right) \\ \end{align} $$ |
| Oscilador libre amortiguado con amortiguación de tipo $\vec{F}=-b\vec{v}$ | $\ddot{x} + 2\gamma\dot{x} + \omega_0^2 x = 0$ |
Dependiendo del nivel de amortiguamiento puede haber tres soluciones distintas:
|
| Oscilador forzado no amortiguado | $\ddot{x} + \omega_0^2 x = \frac{F_0}{m}\cos(\omega t)$ |
$ x(t) = x_h(t) + x_p(t) $ $x(t) = B\cos(\omega_0 t + \beta) + C\cos(\omega t)$ $C=\frac{F_0/m}{\omega_0^2 - \omega^2}$ |
| Oscilador forzado amortiguado | $\ddot{x} + 2\gamma\dot{x} + \omega_0^2 x = \frac{F_0}{m}\cos(\omega t + \alpha_0)$ |
La solución es la suma de un término evanescente y de
otro permanente $ x(t) = \color{blue}{x_h(t)} + \color{green}{x_p(t)} $ $ x(t) = \color{blue}{C e^{-\gamma t}\sin(\omega_\gamma t + \delta)} +\color{green}{ A \sin(\omega t + \alpha_0 + \beta) } $ $\omega_\gamma = (\omega_0^2 - \gamma^2)^{1/2} $ $ A = \frac{F_0/m}{\sqrt{(\omega^2-\omega_0^2)^2 + 4\gamma^2\omega^2}} $ $\beta = -\arctan(\frac{\omega^2 - \omega_0^2}{2\gamma\omega})$ $C$ y $\delta$ son funciones de la posición y la velocidad inicial. |