Difracción
Fuente lineal coherente
Es un artificio matemática útil para estudiar la difracción en otros tipos de aberturas. Dependiendo de cómo aproximemos $r$ tenemos dos tipos de difracción:
- si $r \approx R - y\sin(\theta)$ (lineal en $y$) tenemos la aproximación de Fraunhofer
- si $r = R - y\sin(\theta) + (y^2/2R)\cos^2(\theta) + \ldots$ tenemos la aproximación de Fresnel, que es mucho más compleja
Difracción de Fraunhofer
Difracción de Fraunhofer de una fuente lineal coherente
$$ E = \frac{\epsilon_L D}{R} \frac{\sin(\beta)}{\beta}\sin(\omega t - kR) \qquad \text{con} \qquad \beta = \frac{kD}{2}\sin(\theta) $$ siendo $\epsilon_L$ la eficacia de fuente por unidad de longitud, $R$ la distancia desde el centro de la fuente lineal al punto de observación, $r$ es la distancia de la fuente elemental al punto de observación, $\theta$ la coordenada angular de posición del punto de observación y $D$ la longitud de la fuente lineal (anchura de la rendija). Es decir, el máximo de irradiancia $I=k <E^2>_T$ de una fuente lineal (para $\theta = 0$) es proporcional a su longitud $D$.
Difracción de Fraunhofer de N rendijas rectangulares
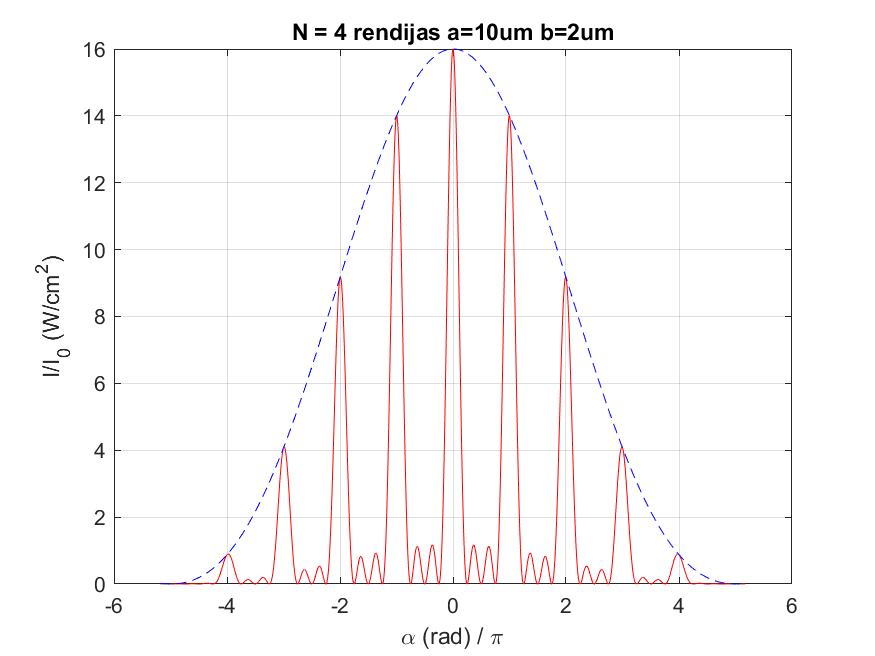
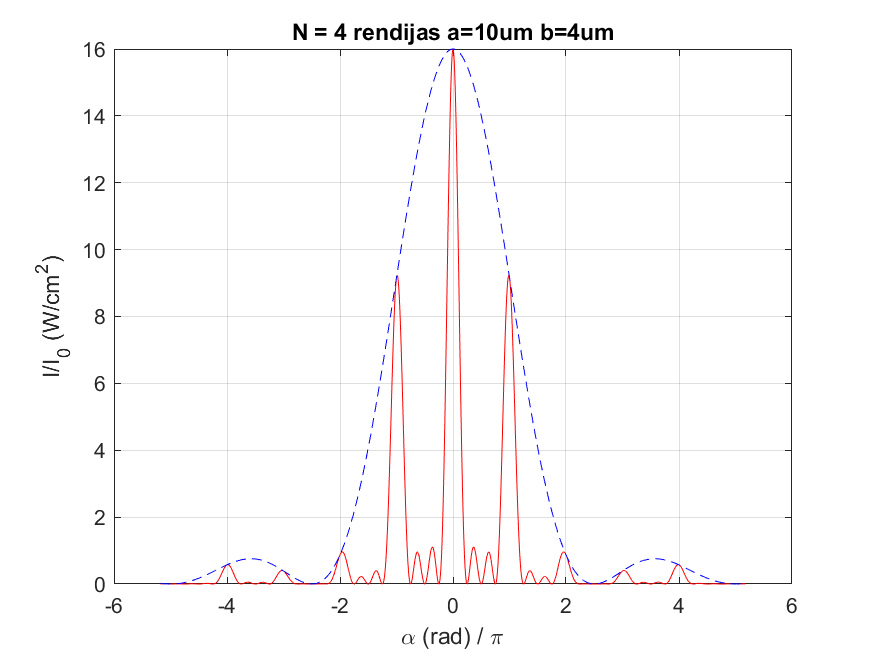
Sean N rendijas (rectángulo muy alargados) de anchura $b$ equiespacidas siendo $a$ la distancia entre sus centros. La irradiancia de este caso general es $$ \begin{align} I(\theta) = I_0 \color{blue}{ \frac{\sin(\beta)}{\beta} } \color{red}{ \frac{\sin(N \alpha)}{\sin(\alpha)} } \color{black}{ \qquad \text{con} \quad \alpha = k\frac{a}{2}\sin(\theta) = \frac{\pi a}{\lambda} \sin(\theta) \quad \text{y} \quad \beta = k\frac{b}{2}\sin(\theta) = \frac{\pi b}{\lambda} \sin(\theta) } \end{align} $$ Para el caso particular $N = 1$, el término interferencial desaparece. Para el caso particular $N = 2$ el término interferencial es (desarrollando el seno del ángulo doble) el familiar $4\cos^2(\alpha)$.
La irradiancia $I(\theta)$ tiene, considerando únicamente el término interferencial
- máximos principales periódicos de amplitud $I_0 N^2$, cuando $a\sin(\theta_m) = m\lambda$, es decir, cuando $\alpha=m\pi$
- $N-2$ máximos secundarios de amplitud, que van disminuyendo en amplitud hasta llegar a medio camino entre los máximos principales, y luego vuelven a aumentar nuevamente, estos máximos varian en amplitud pero en ningún caso sobrepasan el 1/22 parte de los máximos principales
- $N-1$ ceros entre máximos principales, cuando $\alpha=m \pi/N$ con $m = 1, 2, \ldots, N-1, N+1, \ldots$
- todo ello ocurre bajo la envolvente de difracción (normalmente $\beta$ varia mucho más lentamente que $\alpha$ así que dentro del lóbulo principal de difracción hay varios máximos principales, secundarios y nulos de interferencia)
Difracción de Fraunhofer de una abertura rectangular
Difracción de Fraunhofer de una abertura circular
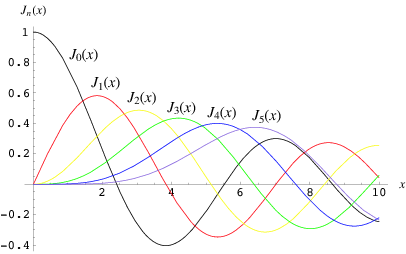
El término difraccional viene dado por la función de Bessel de orden 1 $J_1(\rho)$ $$ I(\theta) = I_0 \left[ \frac{2J_1(\rho)}{\rho} \right]^2 \quad ; \quad \rho = \frac{2\pi}{\lambda}a\sin(\theta) $$ Por la regla de L'Hôpital, $J_1(\rho)/\rho = 1/2$ en $\rho = 0$. Por lo tanto el término difraccional vale 1 en el origen ($\theta = 0$). El 84% de la potencia se halla dentro del disco de Airy y el 91% dentro del segundo anillo oscuro.

Difracción de Fraunhofer de N agujeros circulares
Presenta el término difraccional propio de un agujero circular de radio $a$ y un término interferencial propio de una red de difracción de N elementos difractantes con paso $d$ $$ I(\theta) = I_0 \color{blue}{ \left[ \frac{2J_1(\rho)}{\rho} \right]^2 } \color{red}{ \frac{\sin(N \alpha)}{\sin(\alpha)} } \quad \color{black} ; \quad \rho = \frac{2\pi}{\lambda}a\sin(\theta) \quad ; \quad \alpha = \frac{\pi d}{\lambda}\sin(\theta) $$
Resolución de los sistemas ópticos